达拉斯联储：哪个核心通胀率指标更可靠？是切尾均值消费物价指数还是核心消费物价指数？

本文来自微信公众号“市川新田三丁目”，作者Jim Dolmas和Evan F. Koenig，原标题《Which Core to Believe? Trimmed Mean Versus Ex-Food-and-Energy Inflation》。

Jim Dolmas

Evan F. Koenig

2014年以来，美国个人消费开支物价指数PCE的核心值即不含食品和能源物价变动因素的通胀率，曾两次出现大幅下滑，几乎每次都是到了最后时点才扭转颓势。与此同时，达拉斯联储编制的切尾均值消费物价指数却非常准确地判断出这两次通胀增速的下跌为临时性的，见下图1。

何为切尾均值？

在一个数列中，去掉两端的极端值后的算术平均数。比如在电视上看到歌手大奖赛或体育比赛中常见的“去掉一个最高分，再去掉一个最低分，最后得分是××分”就是利用切尾均值方法进行的评分。

由于算术平均数容易受到数据系列中极端值的影响，因此在对数据大小排序后，按照一定比例去掉最两端的数据，只使用中部的数据来求平均数。如果切尾均值和整体数据的算数均值相差不大，则说明该数据系列不存在极端值，或者两侧极端值的影响正好抵消；反之，则说明数据系列中有极端值，此时切尾均值能更好地反映数据的集中趋势。

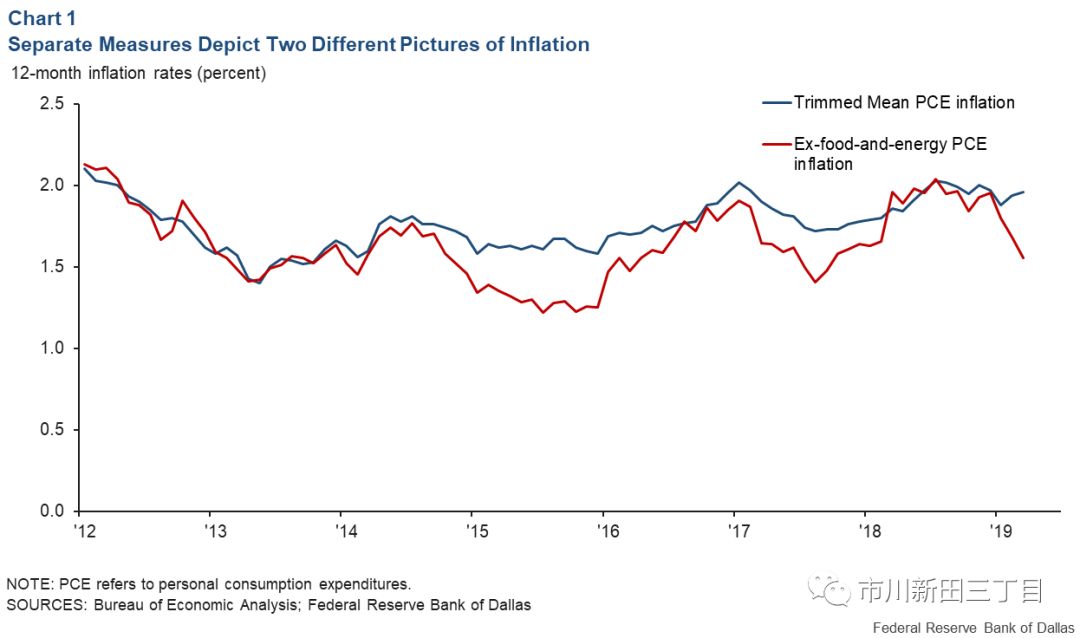
如果在不同的通胀指标中同一类商品或服务的价格所占的权重不一致会导致施策依据相差甚远。近期的物价数据表明各类通胀指标之间再一次出现了偏离，各指标发出的信号自相矛盾导致对切尾均值消费物价指数的关注度出现上升。

我们认为切尾均值消费物价指数消除了月度商品和服务类消费物价中极端波动的数据，因此与不含食品和能源价格涨幅的核心消费物价指数相比能更及时地反映包括食品和能源价格在内所有物价的变动趋势。沿着这个思路，下面来探讨一下切尾均值消费物价指数的诞生原因以及如何构成等话题。

在后文中，我们将应用我们近期所做的一些研究成果，我们会发现切尾均值消费物价指数与不含食品和能源价格涨幅的核心消费物价指数相比所独具的另一个优点，即切尾均值消费物价指数受周期变动的影响更小，数值表现更稳定。

切尾均值消费物价指数产生的原因

为了搞清楚产生的原因，有必要更全面地对核心通胀指标审视一番。

大多数的央行在阐述其各自的通胀目标时用的是涵盖一切的物价指数，但物价指数涵盖一切就有可能变动剧烈，甚至将物价波幅用12个月进行平摊也存在这个问题。此外，大部分的物价波幅与经济的周期性变化或央行所采取的政策并无关联。

涵盖一切的物价指数的剧烈波动有可能会让货币政策的制定者们无从分辨出经济的周期性变化对通胀产生的影响，或者反过来说，很难从通胀数据中推算出经济周期性变化所带来的影响。在这方面，核心通胀指标由于能消除源自物价极端波动的噪音因此可以更好地揭示出经济周期性变化发出的信号。

最为人所熟知的核心通胀指标是不含食品和能源价格涨幅的。决定联储货币政策的联储公开市场委员会定期提交对全部个人消费开支物价指数以及此类核心物价指数的预测报告。

不含食品和能源价格涨幅的核心物价指数的目标很直观，食品和能源类价格的涨幅通常很剧烈，经常与经济的实际情况不相干。但是，深挖一下以下这些物价数据就知道，只是简单粗暴地将所有的食品和能源类价格的涨幅刨除在外并不能有效地消除全面物价指数中包含的噪音。

下图2显示的是，在个人消费物价指数的构成中全部178项物价的月度物价环比波幅，按照物价涨幅大小从左到右进行排序。我们将各类物价的涨幅分成四个档，某一类物价的月度涨幅测算方法用的是四分位距法，即计算全部物价涨幅中位于从小到大排列后第25%的数值与位于第75%的数值之间的差值。差值越大说明各类物价的波幅差距越大。

四分位数也称四分位点，是指在统计学中把所有数值由小到大排列并分成相等的四部分，其中每部分包括25%的数据，处在各分位点的数值就是四分位数。该方法多应用于统计学中的箱线图绘制。如果将全部数据分成相等的两部分，它就是中位数；如果分成四等分，就是四分位数；八等分就是八分位数。四分位数有三个，分别用Q1、Q2、Q3表示。

第一四分位数 (Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字。

第二四分位数 (Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字。

第三四分位数 (Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距（InterQuartile Range,IQR）。

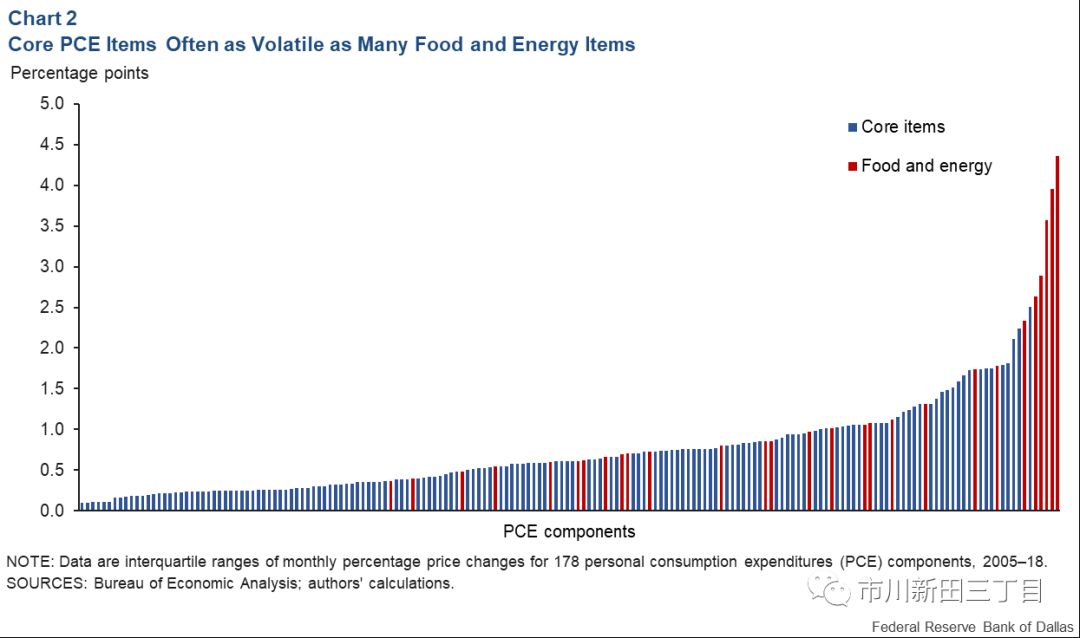
除了占据各类物价涨幅的前几名以外，一些食品和能源类物价的涨幅还与非食品和非能源类物价的涨幅交织在一起。实际上，有14%的食品和能源类商品的物价涨幅低于常见的非食品和非能源类商品物价的涨幅，同样，也有14%的非食品和非能源类商品物价的涨幅超出一些常见的食品和能源类物价的涨幅。

将全部食品和能源类物价的涨幅刨除在外会错失一些波动率不大的食品和能源类价格发出的信号，并导致一些波动率较大的非食品和非能源类价格发出的噪音被包括在物价指数中。而切尾均值计算法则会将月度波幅最大的物价消除在外，而不管该物价所属的大类如何。

一个更有说服力的理由是如果观察到月度物价波幅分布呈现“肥尾”现象，而非正态分布的钟形曲线，说明物价涨幅处于高低两端的情况会很多。统计学的传统理论告诉我们，如果波幅分布呈现“肥尾”现象，那么样本数据的均值，即本例中所有月度物价波幅的算数平均值，将偏离分布的集中趋势或典型值。该理论认为如果将极端值从数据系列中剔除出去得出来的均值会降低噪音信号造成的影响。

如何编制切尾均值消费物价指数？

达拉斯联储在用切尾均值法计算月度通胀增速时用的是美国经济分析局公布个人消费物价指数中178项商品或服务的价格。先是算出来各类物价环比前月的波幅，然后再按照从低到高的顺序排序。比如2019年3月物价剧烈波动的项目有两个，税收筹划的金额按年率计算下跌了62%，而手表的价格按年率计算则上涨了138%。

价格波幅排序完毕后，去掉波幅最低的24%和波幅最高的31%。当月的切尾均值消费物价指数，是根据各价格在整个物价指数中的权重，对涨跌幅度位于中间位置上的各项商品和服务的价格，进行加权平均计算出来的。

通过去掉波幅最低的24%和波幅最高的31%的物价变动项就得出来一个新的通胀率指标，最大限度地体现了包含所有物价变动情况的个人消费物价指数的走势。自2009年最后一次修订后，24%和31%这两个比例就固定不变了。

切尾均值消费物价指数是一种波动更平滑，倾向性更小的实时物价指数

那么，用这种方法得出来的是一种什么样的通胀指标呢？正如人们所预料的，切尾均值消费物价指数比全物价指数或不含食品和能源价格的物价指数的波动率都小。在1993-2008年期间，用四分位距法计算的月度切尾均值消费物价指数的年化波幅只有0.8%，而不含食品和能源价格的物价指数的年化波幅为1.3%，全物价指数的年化波幅为2.3%。

此外，切尾均值消费物价指数的初值，即一经计算完成即对外发布、未经后期修正的数值，是来源于最新出炉的所有物价的涨跌幅度，总体上看其倾向性要小于不含食品和能源价格的物价指数的初值。之所以要强调初值是因为，物价涨幅的初始值是联储公开市场委员会的各位议息委员在做决策时候的数据依据。

切尾均值消费物价指数的初值于2005年开始公布，自那时至今，美国全物价指数的季度增速的平均初值为1.77%，而切尾均值消费物价指数的季度增速的平均初值为1.78%，不含食品和能源价格的物价指数的季度增速的平均初值为1.61%。

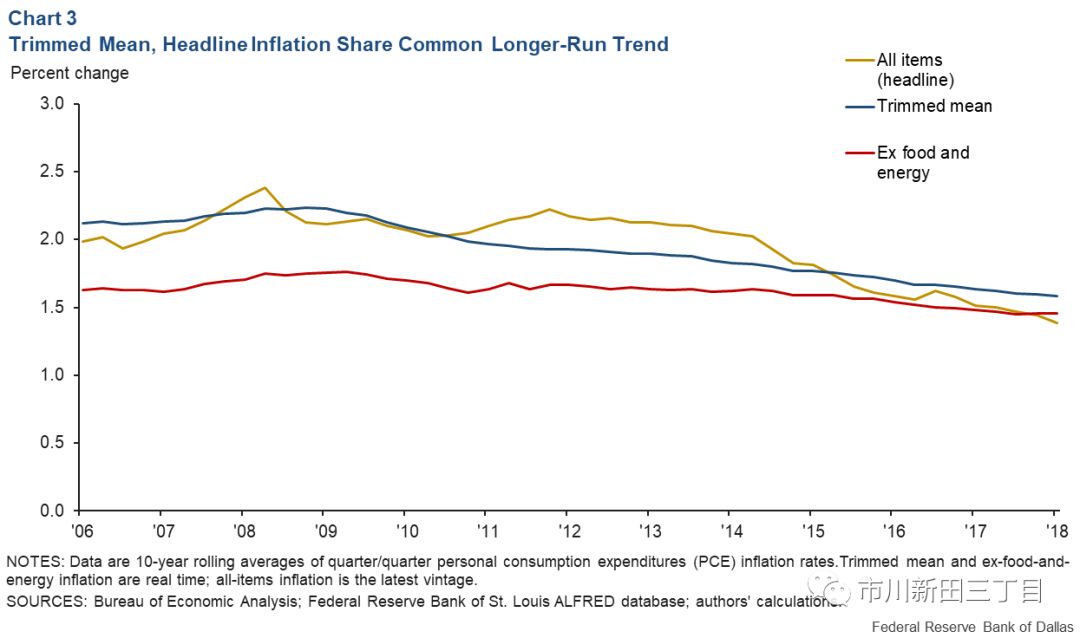
虽然切尾均值消费物价指数高于或低于全物价指数的时候都有，但不含食品和能源价格的物价指数低于全物价指数的时情况更多，见下图3。切尾均值消费物价指数所表现出来的波动率更小、倾向性更低等特点正是其指数构成方法所带来的。

（编辑：孔文婕）